Compressing strings with FSST

We’ve released our Apache-licensed implementation of FSST, you can check it out on GitHub!

Vortex is our open-source Rust library for compressed Arrow. If you want to have compressed Arrow arrays on-disk, in-memory, or over-the-wire, Vortex is designed to help out.

Vortex opts for a columnar representation that is the same both on-disk and in-memory, relying on a set of lightweight compression schemes that allow readers to just-in-time decompress the data you need, when you need it. We’re building out a toolkit of open codecs to efficiently and effectively compress the widest range of data.

Our initial focus has been on numeric codecs, and we’ve written about our approach using the FastLanes layout to compress integers at the bleeding edge of what’s possible on today’s hardware. We’ve also implemented ALP to compress floating point arrays, as well as Roaring Bitmaps.

However, not all data is numeric. String data is incredibly prevalent in the real world. Apache Parquet, the most popular analytics data format, supports compressing strings with dictionary encoding, along with a range of general purpose compressors, which as we see later can be too heavyweight for use cases that favor random indexed access to data.

More recently, there’s been renewed interest within the research community around string compression in databases, and in this post we’re going to describe a relatively new codec called FSST. FSST is fast–the reference implementation achieves gigabytes-per-second decoding–and has shown to compress on average by a factor of 2-3x on many real-world datasets. We're open-sourcing a Rust crate for FSST, and we've also integrated it into our Vortex toolkit.

The next few sections provide a brief history of string compression, motivating the need for a new lightweight string codec like FSST, and then provides a walk through of the steps for compression and decompression.

String compression, in brief

String compression algorithms are not new, and you may already be familiar with some of the more common ones such as Zip, LZ4, and Zstd. All of these operate over blocks of data. Accessing individual values require decompressing the whole block. If you're processing an entire block at a time, this may amortize out, although recent research has shown that due to increasing network and disk bandwidth, reading these formats has become increasingly CPU bound.

The CPU overhead of reading block-compressed data is especially apparent in applications that do lots of small random accesses across a column. Let's take as an example an array with fixed 128KB blocks :

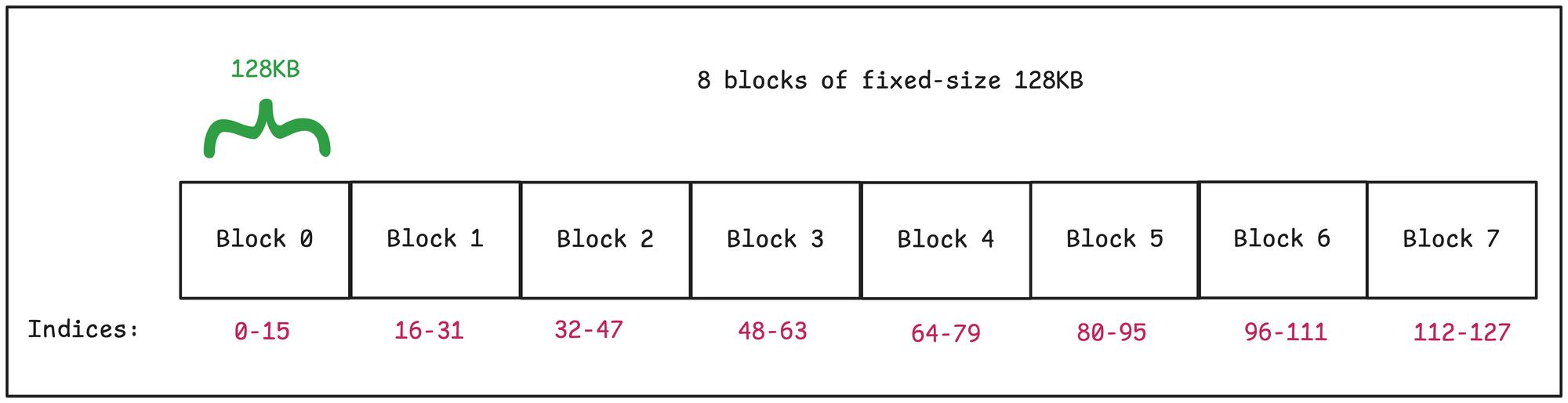
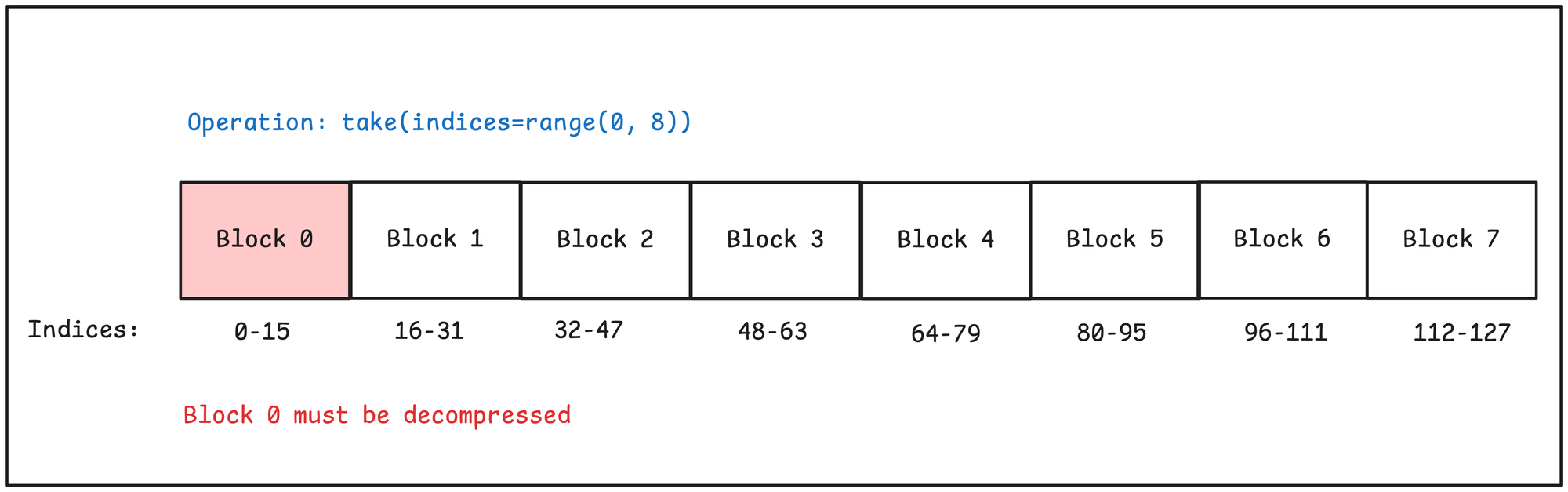
Let's say to service a particular query, we want to access 8 values, or ~6% of the data in the array. In the best case–when the indices are clustered–we can do so by only decompressing a single block.

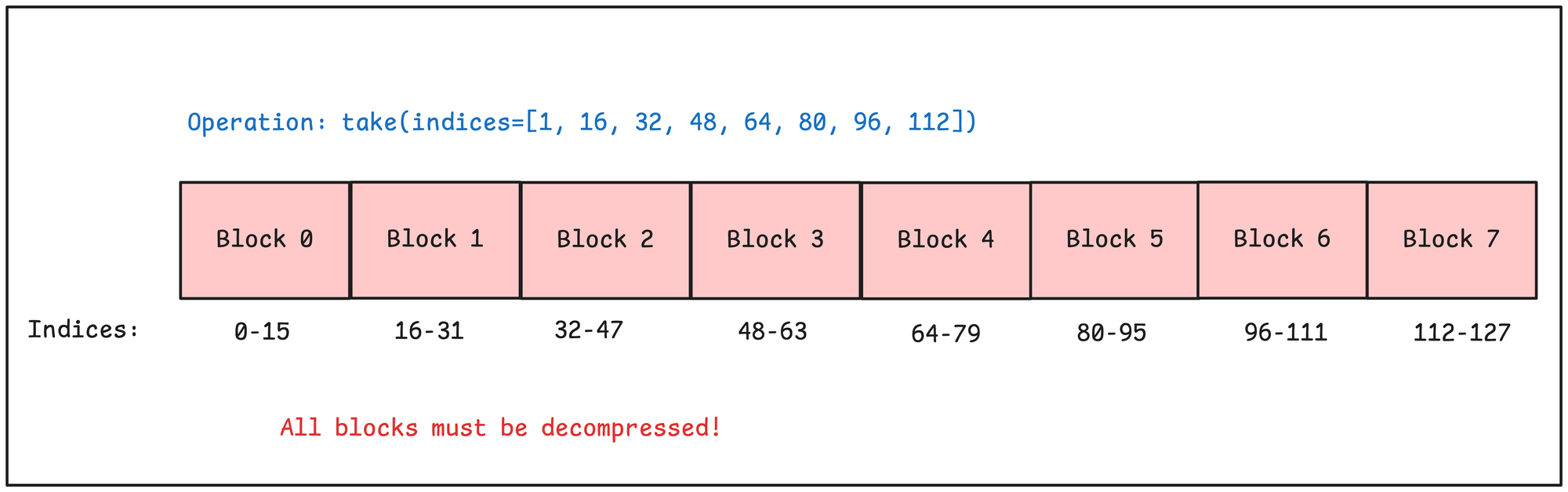
However, if the indices are unclustered and spread out, then in the worst case we must decompress the entire array!

What we want for these more dynamic applications are codecs that support random access. We want a data structure that efficiently implements the following interface:

pub trait StringCodec {
  /// Decode and return the string at the given index.
  fn decode(index: usize) -> String;
}

This is a deep oversimplification of course, but a helpful one for demonstration purposes. We’ll revisit this toy trait throughout the rest of the post to illustrate how random access is implemented for different encoding schemes.

Dictionary Encoding

Dictionary encoding is probably the most well-known codec that supports efficient random access.

It is also one of the simplest: perform a single pass over your data to find the unique values, assign each value an integer code, and replace each occurrence of that value with the code.

We can illustrate with a simple example that has 3 unique strings:

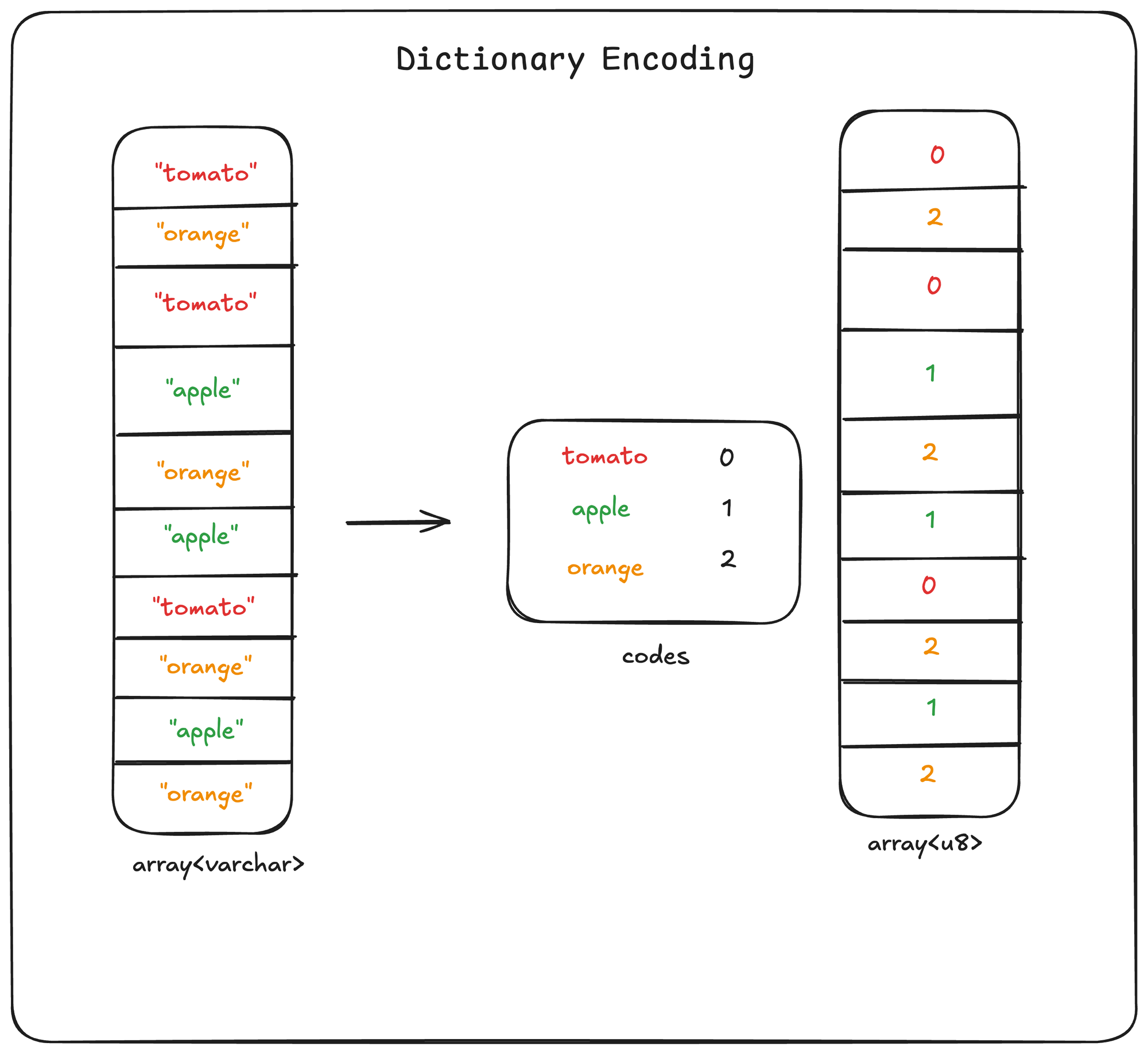
Implementing the single-element decoding just requires access to the dictionary:

pub struct DictionaryArray {
    /// The string at index `i` is replaced with the code `i`.
    /// Stored a single time at the top of the file.
    codes: Vec<String>,
    /// The encoded values. Each string is represented by
    /// an 8-byte code which is an index into the `codes`
    /// table.
    array: Vec<usize>,
}

impl StringCodec for DictionaryArray {
    fn decode(&self, index: usize) -> String {
        // Step 1: lookup the code in the `index` position
        let code = self.array[index];
        // Step 2: map the code back to a string
        self.codes[code].clone()
    }
}

Dictionary encoding is simple, and it performs excellently on many real-world datasets, particularly for categorical columns such as labels and event names. However, it’s not without its drawbacks:

1. Dictionaries only operate at the level of entire strings. If you have repetition that only manifests at the substring level, dictionary encoding won’t help you.
2. Dictionaries only compress well if your data is low-cardinality. As the number of unique values approaches the length of the array, dictionary compression becomes useless, and if you’re not careful it can even be larger than the raw dataset. This is especially pertinent for request logs, JSON records, UUIDs, and free text.
3. You cannot use dictionary encoding to compress data that is not in the dictionary; you instead need to build a new dictionary from scratch. This comes up if you’re building a system that cares about fast append operations, and appending chunks to an existing column with a shared dictionary is desirable.

FSST has entered the chat

The folks over at CWI in the Netherlands & TUM in Germany have been studying databases for a long time, and in 2020 they dropped another banger: FSST: Fast Random Access String Compression. FSST stands for “Fast Static Symbol Table”, a new data structure to act as the backbone for fast random-access string compression.

Putting the ST in FSST

Compressing text with FSST requires you to first build a symbol table, which like a dictionary is shipped with the actual data to be used at decoding time. Unlike dictionaries, which only hold whole-strings, the symbols in a symbol table are short substrings that can occur anywhere in the array. Because most computers have a native 64-bit word size, we say that a symbol can be between 1 and 8 bytes so that it will always fit in a single register.

To make it easy to pass FSST-encoded data around wherever string data would usually go, we set a max table length of 256. This ensures that all codes can be packed into a single byte, allowing our encoding to receive a slice of u8 and return a slice of u8.

Compression works string-by-string, and proceeds greedily, matching the longest prefix against the symbol table, and recording the corresponding code into our output array.

Figure 1 in the paper has an example of what this looks like in practice for a small URL dataset:

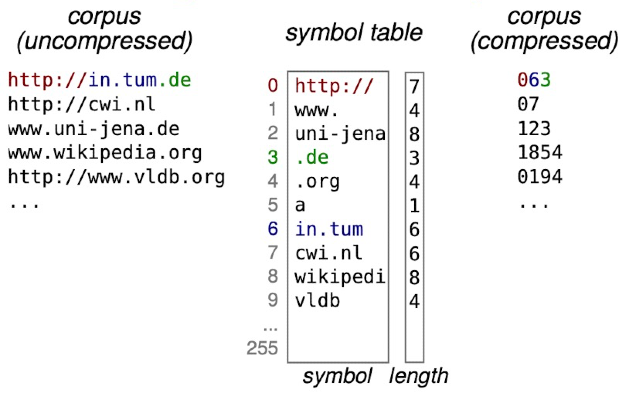
256 codes is a lot, but even with an ideal symbol table, you aren't guaranteed to be able represent any possible string. For that, we need to reserve code 255 (0xFF) to represent the escape code. If while compressing we encounter a substring that does not match any symbol in the table, then we emit each byte of the substring preceded by an escape byte. When the decompressor sees 0xFF in the input, it knows to immediately emit the following byte without looking it up in the symbol table.

If you’re following along, you’ll realize then that the worst-case compression factor is actually a doubling of the input, which we see if we attempt to compress using an empty symbol table.

For example, the string “hello” would be compressed into the byte string:

[0xFF, b'h', 0xFF, b'e', 0xFF, b'l', 0xFF, b'l', 0xFF, b'o']

Based on this, we can start to sketch out the codec and array implementations we’d need to implement FSST decoding with random access:

struct FSSTArray {
    /// `symbols` stores the symbol table. Each symbol can be a string
    /// of 1 to 8 bytes, which we pack into a u64.
    symbols: Vec<u64>,

    /// The length of each symbol. This vector has the same length
    /// as `symbols`.
    symbol_lengths: Vec<u8>,

    /// The encoded variable-length byte array. bytes[i] is the i-th encoded
    /// string.
    ///
    /// Each encoded string will be a sequence of 8-bit unsigned
    /// integer offsets into the `symbols` table.
    bytes: Vec<Vec<u8>>
}

impl StringCodec for FSSTArray {
    fn decode(&self, index: usize) -> String {
        // Get the compressed value at the index.
        // This is a byte array of codes.
        let codes = self.bytes[index];
        let mut pos = 0;
        let mut result = Vec::new();
        while pos < codes.len() {
            let next_code = codes[pos];
            if next_code == ESCAPE {
                // Emit an escape byte
                pos += 1;
                result.push(code[pos]);
            } else {
                // Lookup the code in the symbol table
                let symbol = self.symbols[code];
                let len = self.symbol_lengths[code] as usize;
                result.extend_from_slice(&symbol.to_le_bytes()[0..len]);
            }

            pos += 1;
        }
		
        // Convert the UTF-8 encoded bytes into a String for the caller
        String::from_utf8(result).unwrap()
    }
}

Based on these characteristics, we can quickly see that the theoretical compression factors range from 8—the maximum length of a symbol—to 0.5 in the case where every byte of a string is escaped. Thus, building a symbol table to preference long-matches and avoiding escapes is going to be key to both good compression factors and fast decompression speeds.

A seat at the (symbol) table

FSST compression relies on a generational algorithm for building a symbol table. In each generation, it uses the current generation’s symbol table to compress a piece of sample text, then examines the used codes to create a set of new potential candidate symbols. At the end of the generation, the best symbols are preserved for the next generation.

We need to be more specific about how we decide the “top” symbols however. In the paper, the author’s define a new metric for the “effective gain” of a symbol. A symbol’s effective gain is equal to its length times its frequency of how it appears in the compressed text. Semantically, this is like the marginal compression factor of having this one symbol in the table, for the given piece of text we’re evaluating against.

The algorithm takes 3 parameters:

• Maximum symbols: how big can the symbol table grow. This is directly linked to the code size. Because we’re using byte codes, this is 255 (leaving the 256th code for an escape).
• Maximum symbol length: How many bytes can each symbol hold? This was chosen to be 8 bytes so that it can always fit into a single 64-bit register.
• Number of generations: How many generations does the table selection algorithm proceed for? Because we concatenate symbols at the end of each generation, we must have at least 3 generations to have a chance to generate any 8 byte symbols. The creators of FSST did a lot of empirical testing and found 5 to provide the best balance between speed and compression quality.

Now that we have all of the parameters of the algorithm, we can be a bit more rigorous in our description of the steps.

First, we initialize an empty symbol table. An empty symbol table will compress any string it receives into a byte array where each character is preceded by an escape byte.

For each generation:

1. We compress our target string using our existing symbol table. When we compress, we count the symbols that were used in the encoded output. We also concatenate adjacent symbols as candidates for new symbols to add.
2. For all existing and candidate symbols, we assign them a gain (count * length), and preserve the top 255 symbols by gain.
3. We set the top 255 as the new symbol table to use in the next generation.

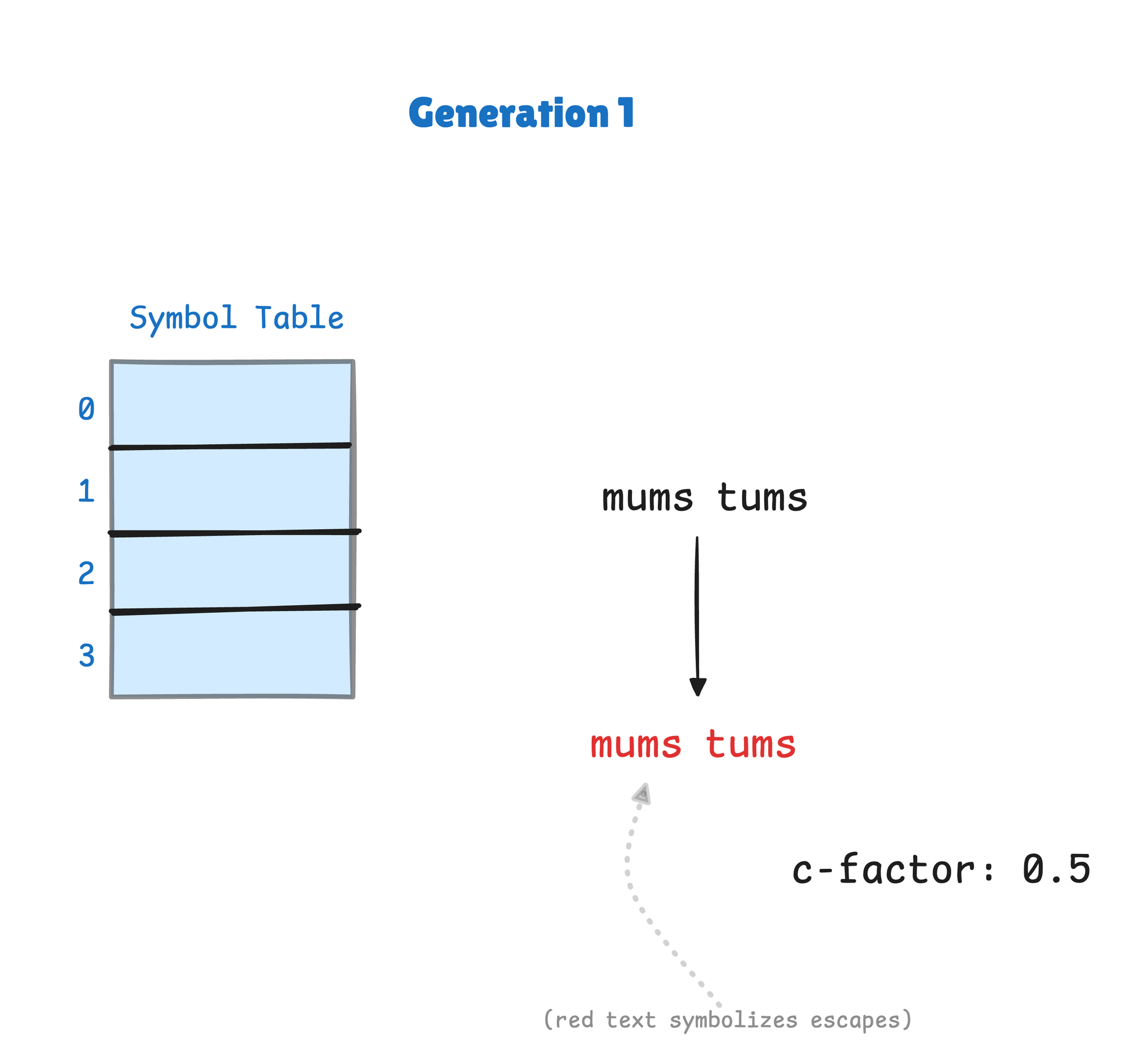
We’ve illustrated a simplified version of the algorithm below. We use a a toy string mums tums , and we’ve altered the parameters to make things fit in one page:

• Maximum symbols: 4
• Maximum symbol length: 3
• Number of generations: 2

First comes Step 1: Compress using the existing symbol table. In this case, the symbol table is initialized to be empty, so this will escape all bytes, doubling the size of the text!

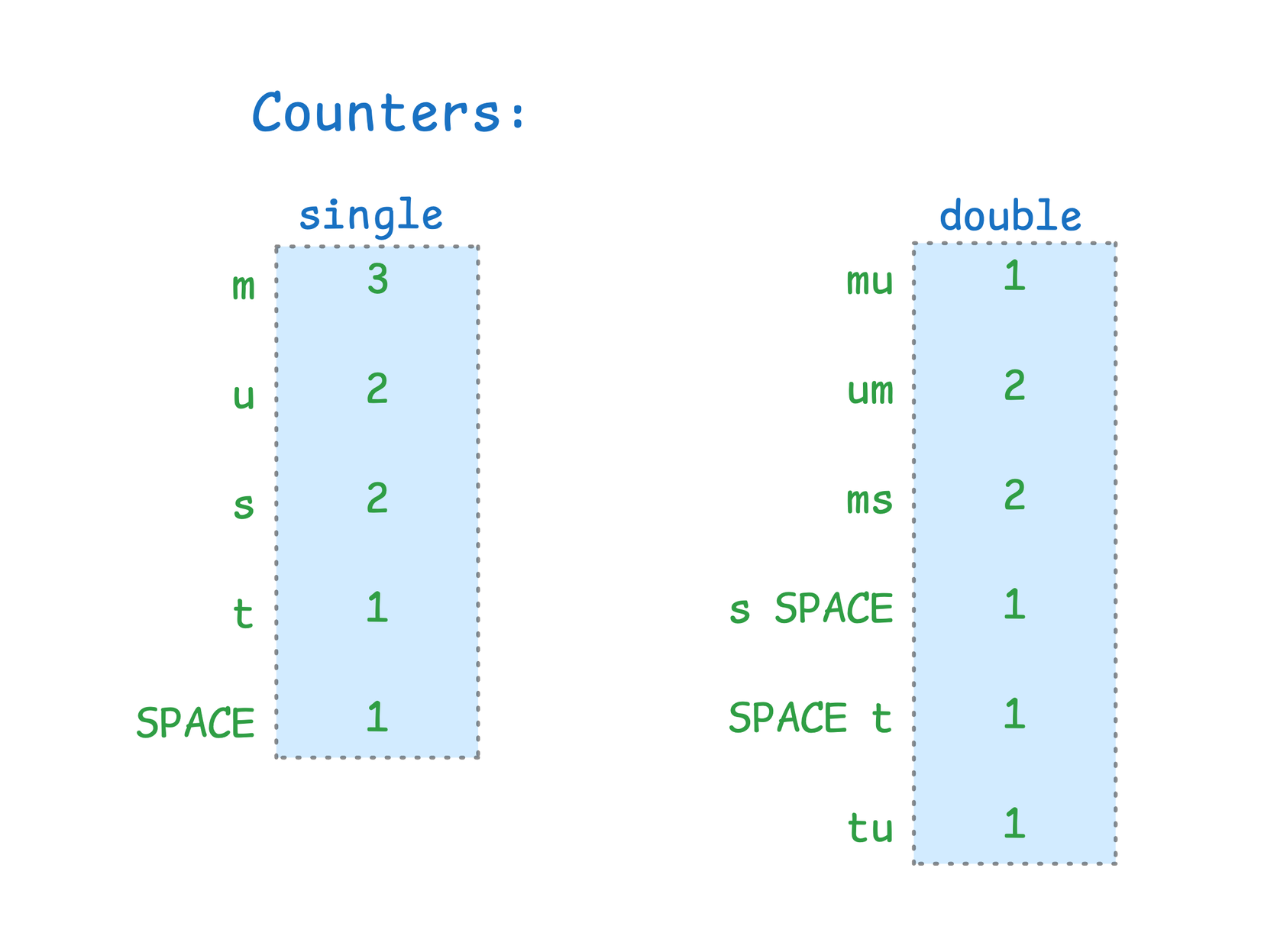
Step 2: Count the symbols that appear in the compressed text. In this case, the symbols are all single-character escapes. We also count all adjacent pairs of symbols that appear, as they are good candidates to merge into a single symbol.

Step 3: Rank the candidates by their effective gain. We preserve the top symbols (in this toy example, the top four) to use as the new symbol table.

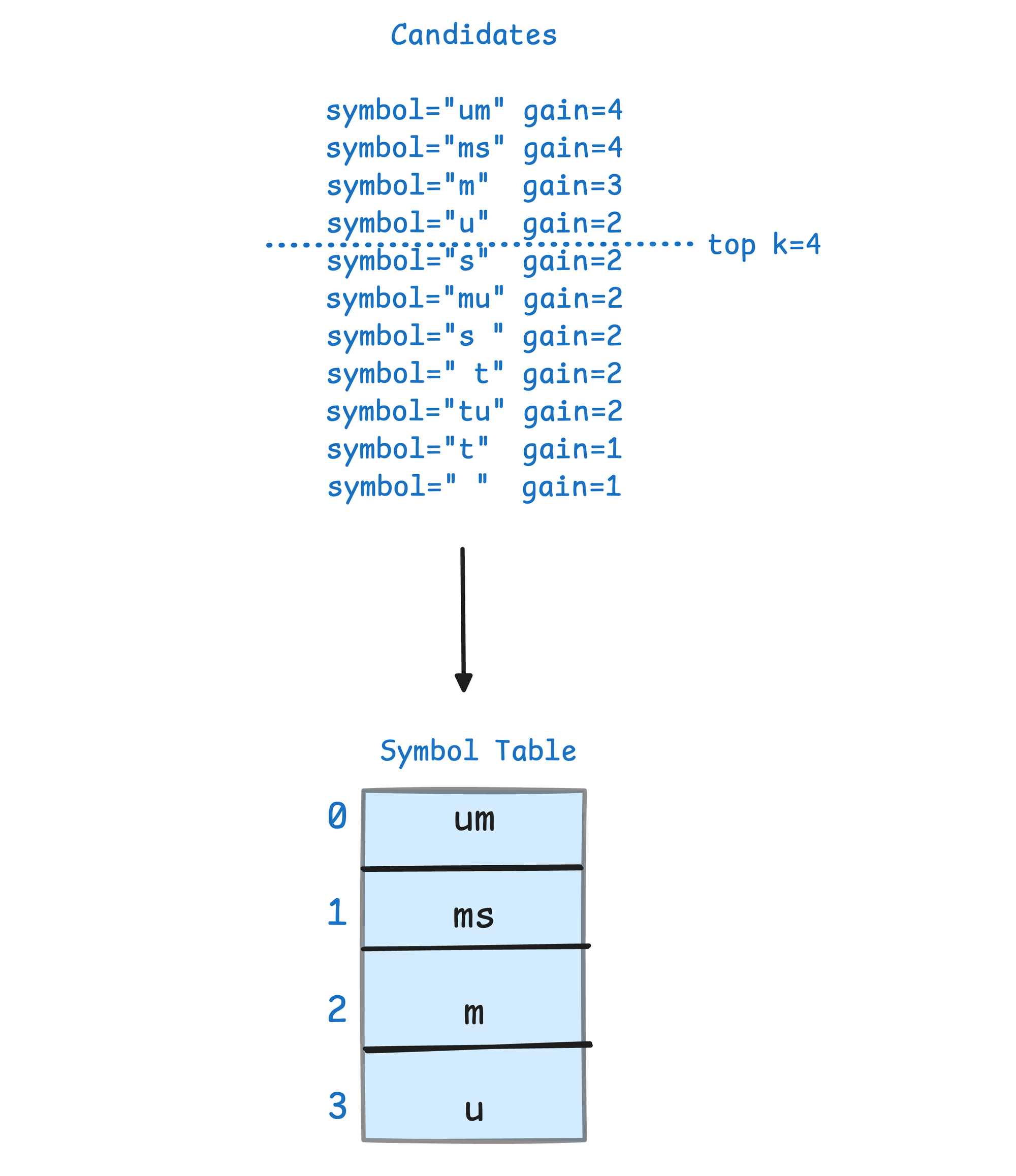
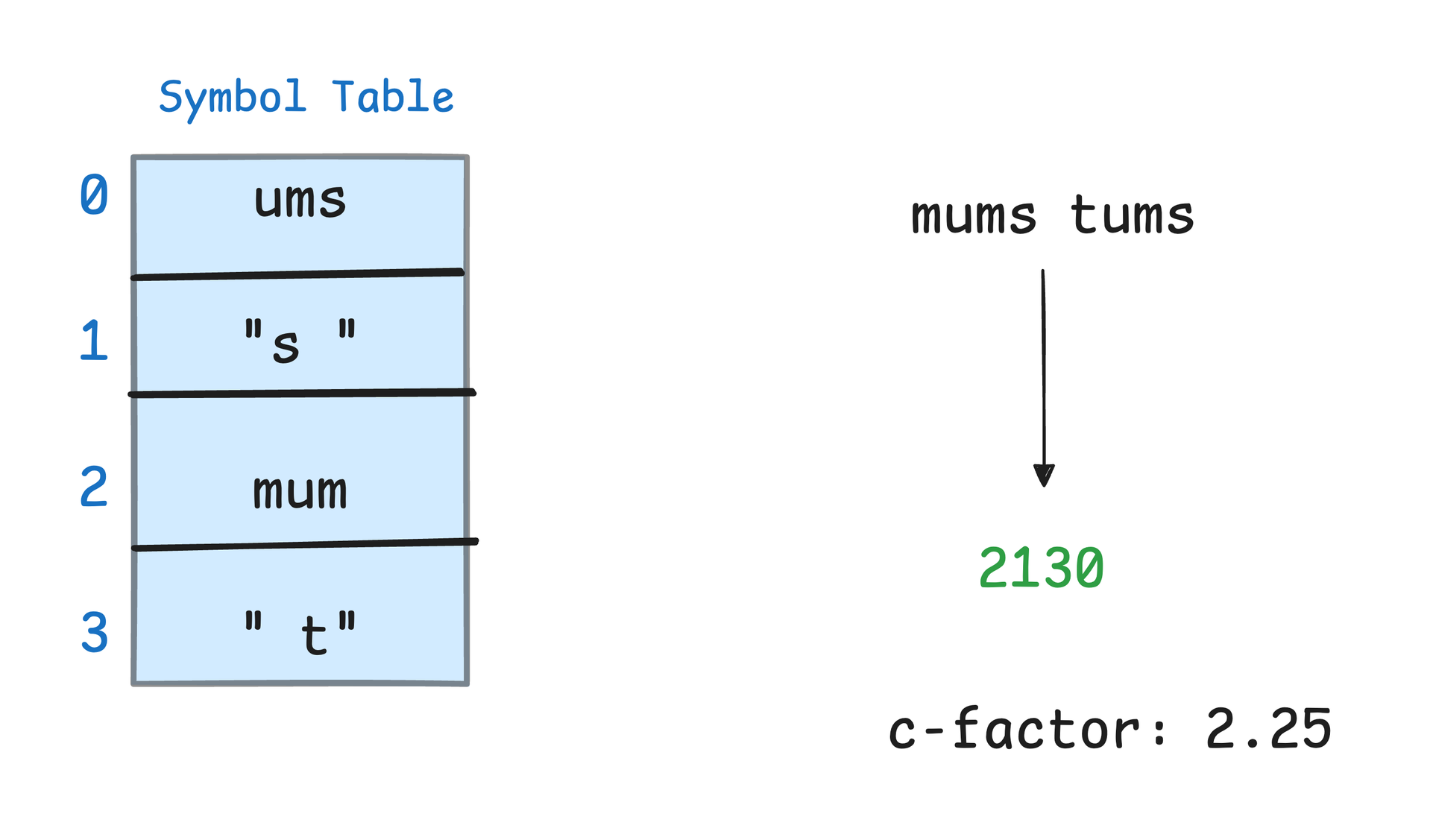
We now have a complete symbol table. We repeat the steps above for the second generation:

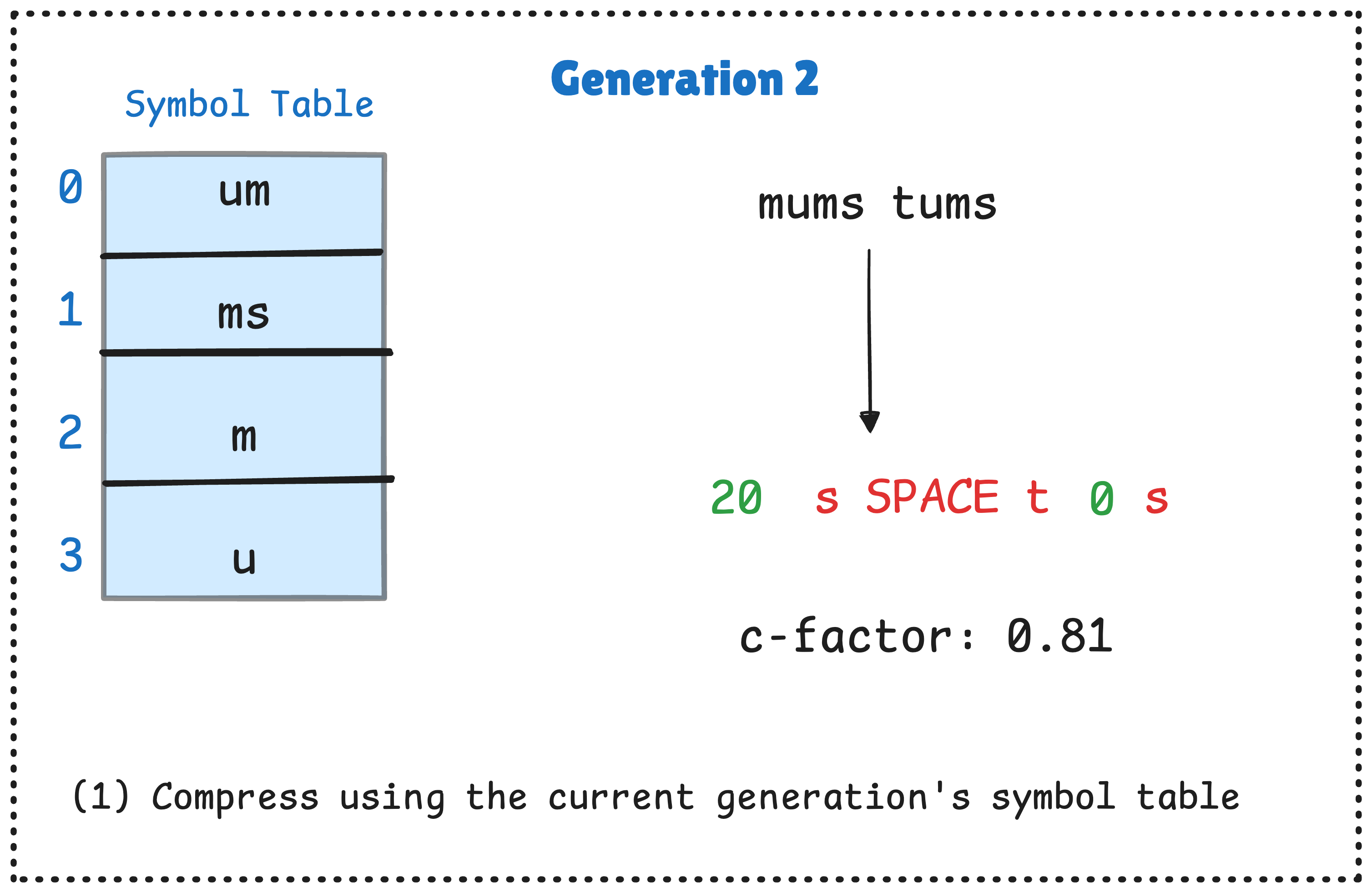
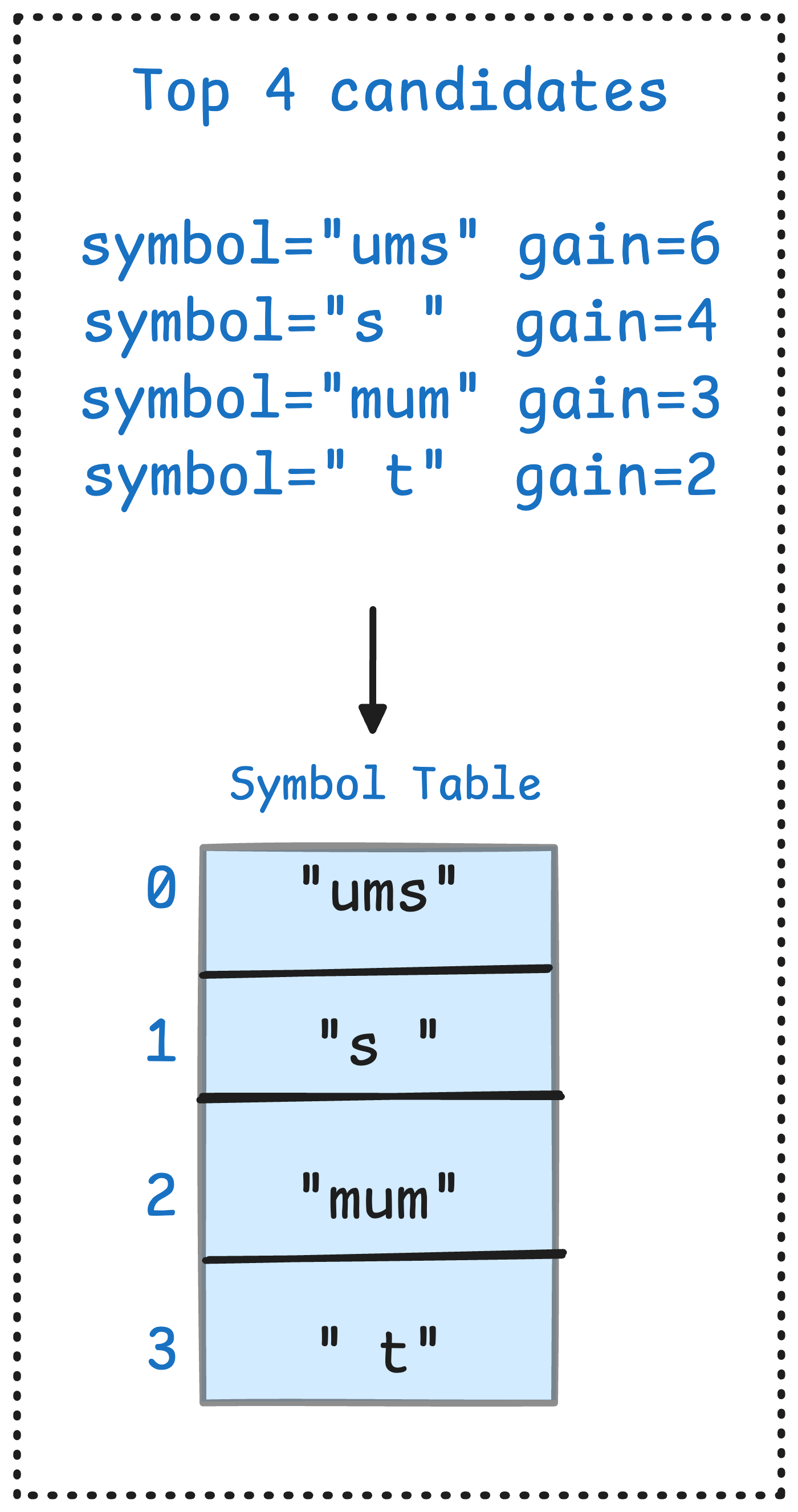
In the first generation, our empty symbol table initially doubles the size of our output, but over two generations we refine this table, arriving at one that actually compresses our string by more than a factor of 2!

As mentioned, this was a simplified example meant to strip away details to clarify the algorithm’s mechanics. There are quite a few moving pieces needed to actually bring this code to life:

1. Extending support from single-strings to string arrays with many values. The naive way to do this is to call the compression/decompression kernels in a loop. A more advanced variant would compress the entire array range as a single mega-string to avoid branching.
2. Training the symbol table on a whole array forces us to compress the full-size array 5 times, which is slow. Instead, we choose a small fixed-size sample of 16KB, drawn as 512B chunks sampled uniformly at random across all elements of the array. Both 16KB and 512 were chose empirically by the authors as good tradeoffs between locality (longer runs are more realistic representations of the source) and performance (getting a diverse enough sample to train a table that compresses the whole array well).
3. The authors of the paper implemented an AVX-512 compression kernel, which we have not implemented in the Rust code but can lead to better performance over the scalar variant. You can learn more about their “meatgrinder” in Section 5 of the paper.

Closing thoughts

For all the ink spilled in this post, there's still so much we didn't get to cover. For that, we encourage you to read the paper as well as the Rust code for more details on the specific tricks needed to make the codec fast enough for use.

We believe that FSST is a great building block for working with string data, and providing a good wrapper around its power brings us closer to achieving our goal of making Vortex the absolute best way to build data-intensive applications. We’re building in the open, so if you’re interested in following along on the journey, be sure to check us out on GitHub!